이번 글에서는 "규제 개념을 가진 릿지모델과 라쏘모델", 이 두가지 회귀모델에 대해 살펴보고자 한다. 이 과정에서 이전에 특성공학을 적용한 다중회귀모델에 비해 릿지 모델이 얼마나 성능 향상을 가져다주는지 비교해 볼 것이다. 또한, 릿지 모델과 라쏘모델 간의 성능 차이도 비교해 볼 것이다. 특히, 성능을 더욱 향상시키기 위한 방법으로 하이퍼파라메터인 알파값을 조정하는 규제 방법을 적용해 보고 그 결과를 공유하려 한다.
(이 전에 작성한 특성공학을 적용한 다중회귀모델에 관한 글을 아래를 참고하시라.)
2023.12.24 - [[파이썬]/머신러닝] - [머신러닝] 특성공학을 활용한 다중회귀모델 성능 향상(+예제, 해석, 개념)
차례와 사용 툴 및 라이브러리는 아래와 같다.
[차례]
첫 번째, 특성 정규화
두 번째, 예제 1: 특성공학을 적용한 다중회귀모델에 릿지(Ridge) 모델 활용하여 성능 향상 시키기
세 번째, 예제 2: 릿지 모델과 성능 비교를 위한 라쏘(Lasso) 모델 활용
네 번째, 하이퍼파라메터 알파값 조정을 통한 라쏘 모델 성능 향상
[사용 툴]
- Jupyter notebook(웹 기반 대화형 코딩 환경)
[사용 라이브러리 및 모듈]
- 머신러닝 라이브러리 및 모델: scikit-learn
- sklearn.preprocessing.StandardScaler: 정규화(표준화) 변환
- sklearn.metrics.mean_absolute_error: 평균절대오차(MAE) 측정
- sklearn.linear_model.Lasso: 라쏘 모델 생성
- sklearn.linear_model.Ridge: 릿지 모델 생성
규제(Regularization)
규제 개념
규제는 머신러닝 모델이 훈련 데이터에 과적합 되는 것을 방지하기 위한 방법이다. 과적합은 모델이 훈련 데이터에 너무 잘 맞아서 새로운 데이터에 대한 예측 성능이 떨어지는 현상을 말하는데, 이를 방지하기 위해 규제를 사용한다. 규제를 사용하면 훈련의 정확도는 다소 낮아질 수 있지만, 검증(테스트) 정확도를 높이는 효과가 있다.
규제 순서
규제를 적용하기 전에는 동일한 스케일(단위)을 갖도록 특성을 정규화한다. 이렇게 하면 모든 특성이 균등하게 비용 함수(오차 혹은 손실을 측정하는 함수)에 영향을 미치게 되어, 규제의 효과를 극대화할 수 있다. 그 후, 규제가 적용된 모델을 훈련하고 검증한다.
규제를 적용한 회귀 모델
- 릿지(Ridge): 이 방법은 모델의 오차를 줄이는 동시에, 가중치의 제곱을 최소화하려고 한다. 이로 인해 모든 가중치가 일정 수준으로 줄어들지만, 0이 되지는 않는다. 이 방법도 모델이 복잡해질 수 있는 과적합을 방지한다.
- 라쏘(Lasso): 이 방법은 모델의 오차를 줄이는 동시에, 가중치의 절댓값을 최소화하려고 한다. 이로 인해 일부 가중치는 0이 되어 결국 모델이 간단해진다. 즉, 중요하지 않은 특성은 모델에서 제외되며, 이를 통해 과적합을 방지한다.
즉, 릿지와 라쏘는 모델의 오차를 줄이면서도 모델이 너무 복잡해지지 않도록 가중치를 제한하는 방법이다. 이를 통해 모델이 새로운 데이터에 대해 더 잘 예측할 수 있도록 돕는다.
특성 정규화
1. 데이터 불러오기
다중회귀모델의 성능을 향상시키기 위해, 특성공학을 적용한 독립변수와 원본 데이터의 종속변수를 사용한다.
train_poly.shape, train_target.shape, test_poly.shape, test_target.shape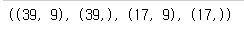
2. 모델 구축
2.1 라이브러리 호출 및 정규화 모델 생성
규제를 적용하기 전, 모든 특성의 스케일(단위)을 동일하게 조정하기 위해, sklearn 라이브러리의 StandardScaler 클래스를 활용하여 정규화 모델을 생성한다. 이 모델은 데이터를 표준화하는 작업, 즉 평균을 0으로, 표준편차를 1로 조정하여 특성의 스케일을 맞추는 역할을 한다.
from sklearn.preprocessing import StandardScaler
ss = StandardScaler()
ss
3. 모델 학습(훈련)
3.1 정규화 모델 학습
정규화 모델에 fit 함수를 활용하여, 데이터의 각 특성(열)의 통계적 특성인 평균(mean)과 표준편차(std)를 학습시킨다.
ss.fit(train_poly)
4. 데이터 전처리
transform 함수를 활용하여 정규화 모델이 학습한 패턴을 기반으로, 훈련 데이터와 테스트 데이터의 독립변수의 스케일(단위)을 모두 동일하게 맞추는 전처리 작업을 수행한다.
train_scaled = ss.transform(train_poly)
test_scaled = ss.transform(test_poly)
print(f" 훈련 독립변수:{train_poly.shape} \n 테스트 독립변수:{test_poly.shape}")
print(f" 훈련 독립변수 스케일: {train_scaled}")
예제 1: 특성공학을 적용한 다중회귀모델에
릿지(Ridge) 모델 활용하여 성능 향상 시키기
1. 모델 구축
1.1 라이브러리 호출 및 릿지 모델 생성
sklearn 라이브러리의 Ridge 클래스를 호출하여, 릿지 모델을 생성한다. 해당 모델은 정규화된 특성을 활용하여, 가중치(계수)의 제곱을 최소화하는 방식으로 가중치(계수)를 제한한다.
from sklearn.linear_model import Ridge
ridge = Ridge()
ridge
2. 모델 학습(훈련)
2.1 릿지 모델 학습
릿지 모델에 fit 함수를 활용하여, 독립변수와 종속변수 사이의 관계를 학습시킴과 동시에 가중치(계수)의 크기를 제한시킨다. 이 과정에서 릿지 모델은 L2 규제를 적용, 즉 가중치(계수)의 제곱을 최소화하여 모델의 복잡도를 제한하고 과적합을 방지한다. 이를 통해 새로운 데이터에 대한 예측 성능, 즉 일반화 성능이 향상되는 데 도움을 준다.
ridge.fit(train_scaled, train_target)
3. 모델 성능 평가
3.1 훈련 및 테스트 데이터 세트의 결정계수 확인
정규화된 독립변수와 일반 종속변수를 가진 훈련 데이터와 테스트 데이터에 score 함수를 적용하여, 릿지 모델의 결정계수를 확인한다.
train_r2 = ridge.score(train_scaled, train_target)
test_r2 = ridge.score(test_scaled, test_target
print(f"훈련 결정계수:{train_r2}, 테스트 결정계수:{test_r2}")
3.1.1 해석
- 릿지 모델의 경우, 훈련 결정계수가 테스트 결정계수보다 0.0004 높게 나타난 것으로 보아 과적합이 발생하지 않은 일반화된 모델로 보임
4. 모델 예측
4.1 테스트 데이터로 예측하기
predict 함수의 인자로 테스트 데이터의 정규화된 독립변수를 전달하여, 모델이 학습한 관계를 기반으로 해당 독립변수에 대한 종속변수의 예측값을 출력한다. 이 예측값은 모델이 학습한 패턴에 기반하여 계산된 것이며, 이를 통해 모델의 성능을 평가하거나, 실제 운영 환경에서 예측을 수행하는 데 사용할 수 있다.
test_pred = ridge.predict(test_scaled)
print(f"모델의 예측값:{test_pred}")
5. 예측 성능 평가
5.1 테스트 데이터로 예측하기
'sklearn.metrics' 패키지의 'mean_absolute_error' 함수는 '평균절대오차(MAE)'를 계산하는 함수이다. 이는 실제값과 예측값의 차이를 절댓값으로 변환한 후 평균을 내는 방식으로, 회귀 모델의 성능을 평가하는 중요한 지표이다.
평균절대오차(MAE) 함수에 실제값과 예측값을 인자로 전달하면, 해당 함수는 각 데이터 샘플에 대한 두 값의 차이(오차)를 절댓값으로 바꾼 후, 모두 합한다. 이 합산값을 샘플의 전체 개수로 나눔으로써 평균을 구한다. 이를 통해, 모델의 예측값과 실제값이 평균적으로 얼마나 차이 나는지를 측정할 수 있다.
from sklearn.metrics import mean_absolute_error
mean_absolute_error(test_target, test_pred)
6. 모델 성능 종합 해석
6.1 특성공학을 적용한 다중회귀모델과 릿지 모델의 성능지표 비교


- 릿지 모델과 특성공학을 적용한 다중회귀모델의 성능지표를 비교해 보면, 릿지 모델의 훈련 결정계수는 0.005 정도 감소하였지만, 테스트 결정계수는 0.013 정도 상승함
- 뿐만 아니라, 평균절대오차(MAE)도 1만큼 감소함
- 이 결과를 통해, 릿지 모델은 특성공학을 적용한 다중회귀모델보다 성능이 뛰어난 모델로 판단됨
예제 2: 릿지 모델과 성능 비교를 위한
라쏘(Lasso) 모델 활용
1. 모델 구축
1.1 라이브러리 호출 및 라쏘 모델 생성
sklearn 라이브러리의 Lasso 클래스를 호출하여, 라쏘 모델을 생성한다. 해당 모델은 정규화된 특성을 활용하여, 가중치(계수)의 절댓값을 최소화하는 방식으로 가중치(계수)를 제한한다.
from sklearn.linear_model import Lasso
lasso = Lasso()
lasso
2. 모델 학습(훈련)
2.1 라쏘 모델 학습
라쏘 모델에 fit 함수를 활용하여, 독립변수와 종속변수 사이의 관계를 학습시킴과 동시에 가중치(계수)의 크기를 제한시킨다. 이 과정에서 라쏘 모델은 L1 규제를 적용, 즉 가중치의 절댓값을 최소화하여 모델의 복잡도를 제한하고 과적합을 방지한다. 이를 통해 새로운 데이터에 대한 예측 성능, 즉 일반화 성능이 향상되는 데 도움을 준다.
lasso.fit(train_scaled, train_target)
3. 모델 성능 평가
3.1 훈련 및 테스트 데이터 세트의 결정계수 확인
정규화된 독립변수와 일반 종속변수를 가진 훈련 데이터와 테스트 데이터에 score 함수를 적용하여, 라쏘 모델의 결정계수를 확인한다.
train_lasso = lasso.score(train_scaled, train_target)
test_lasso = lasso.score(test_scaled, test_target)
print(f"훈련 결정계수:{train_lasso}, 테스트 결정계수:{test_lasso}")
3.1.1 해석
- 라쏘 모델의 경우, 훈련 결정계수가 테스트 결정계수보다 0.0002 낮게 나타난 것으로 보아, 미세한 과소적합의 발생이 의심됨
4. 모델 예측
4.1 테스트 데이터로 예측하기
predict 함수에 테스트 데이터의 정규화된 독립변수를 인자로 전달하여, 라쏘 모델이 학습한 패턴을 기반으로 종속변수의 값을 예측한다.
test_pred = lasso.predict(test_scaled)
print(f"예측값:{test_pred}")
5. 예측 성능 평가
5.1 테스트 데이터로 예측하기
평균절대오차(MAE) 함수에 실제값과 예측값을 인자로 전달하여, 실제값과 예측값이 평균적으로 얼마나 차이 나는지 측정한다.
mae = mean_absolute_error(test_target, test_pred)
print(f"평균절대오차:{mae}")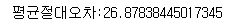
6. 모델 성능 종합 해석
6.1 라쏘 모델과 릿지 모델의 성능지표 비교


- 라쏘 모델과 릿지 모델의 성능지표를 비교해 보면, 라쏘 모델의 훈련 결정계수는 릿지 모델에 비해 0.0012 정도 높게 나타났으며, 테스트 결정계수 또한 0.0018 정도 높게 나타났음
- 더불어, 평균절대오차(MAE) 값은 3만큼 감소하였음
- 이러한 결과를 통해, 라쏘 모델은 전반적으로 나쁜 모델은 아니지만, 훈련 결정계수가 테스트 결정계수보다 0.0002 낮게 나타난 것으로 보아, 이는 미세한 과소적합의 가능성을 보임
- 따라서, 해당 모델의 사용에 있어서는 약간의 미흡한 부분이 있음을 보임
- 이를 해결하기 위해, 라쏘 모델에 하이퍼파라메터 튜닝, 즉 규제를 적용하여 모델의 성능을 개선하고자 함
하이퍼파라메터 알파값 조정을 통한 라쏘 모델 성능 향상
7. 하이퍼파라메터 튜닝
7.1 규제 적용
하이퍼파라메터 튜닝을 위해 모델을 재생성하고, 이 과정에서 알파값, 즉 규제 강도를 조절하게 된다. 알파(alpha)는 모델의 복잡성을 결정하는 중요한 요소이다.
알파값이 높으면 규제 강도가 강해져 모델의 가중치(계수)가 크게 감소한다. 이는 모델이 데이터의 복잡성을 덜 반영하게 만드는 효과를 가져와서, 훈련 데이터에 대한 결정계수를 감소시킬 수 있다. 이 과정은 과대적합을 방지하게 도와주지만, 테스트 데이터에 대한 일반화 성능을 향상시키는 데 도움이 된다.
반면, 알파값이 낮아지면 규제 강도가 약화되어 모델의 복잡성이 증가하고 가중치(계수가) 또한 증가한다. 이는 복잡한 패턴을 더욱 잘 학습하게 도와주지만, 알파값이 과도하게 낮으면 모델이 훈련 데이터에 과적합되는 위험이 있다.
따라서, 교차 검증과 같은 방법을 활용하여, 여러 알파값 중에서 가장 좋은 성능을 보이는 값을 선택하는 것이 일반적인 접근 방식이다. 이렇게 알파값을 적절히 조절함으로써, 모델의 일반화 성능을 개선하고 결정계수를 최적화할 수 있다.
lasso = Lasso(alpha=0.1)
lasso.fit(train_scaled, train_target)
train_lasso = lasso.score(train_scaled, train_target)
test_lasso = lasso.score(test_scaled, test_target)

7.1.1 해석
- 알파값(alpha), 즉 하이퍼파라메터의 조절을 통해, 라쏘 모델의 훈련 결정계수와 테스트 결정계수가 변화하는 것이 확인됨
- 알파값이 0.01에서 0.1로 증가하면서 규제 강도가 강해질 때, 훈련 결정계수는 0.0003 상승하였고, 테스트 결정계수 또한 0.002 상승함
- 그러나 알파값이 0.1에서 1, 그리고 10으로 조정되었을 때에는 훈련 결정계수가 각각 0.002, 0.005 감소함
- 반면, 테스트 결정계수는 알파값이 1일 때 0.001 정도 상승했다가, 10일 때 0.07 감소함
- 알파값이 0.1일 때, 훈련 결정계수와 테스트 결정계수는 각각 0.9883, 0.9857로 가장 높게 나타남
- 따라서, 해당 모델은 과적합이 발생하지 않으면서도 성능이 매우 우수한 일반화 모델로 판판됨
7.1.2 알파값 적용 전후의 라쏘 모델 성능지표 비교


- 최적의 알파값인 0.1을 적용한 결과, 라쏘 모델의 훈련 결정계수는 0.002 증가하였으며, 반면에 테스트 결정계수는 0.0006 감소함
- 그러나 이 감소 치는 훈련 결정계수의 증가에 비해 낮은 수치이며, 알파값 조정 전에는 훈련 결정계수가 테스트 결정계수보다 0.0002 낮은 과소적합의 가능성을 보였으나, 알파값 적용 후에는 이를 해소한 것으로 보임
- 따라서, 하이퍼파라메터 튜닝(알파값 조정)을 적용한 라쏘 모델이 더욱 일반화된 성능을 보이는 것으로 판단됨
이번 글에서는 특성공학을 적용한 독립변수를 정규화(표준화) 처리한 뒤, 릿지 모델에 적용하여 그 성능을 살펴보았다. 릿지 모델과 특성공학을 적용한 다중회귀모델을 비교 분석한 결과, 릿지 모델이 더 우수한 성능을 보이는 것을 확인하였다.
또한, 동일한 독립변수를 라쏘 모델에 적용하여 릿지 모델과의 성능 차이를 비교하였다. 이 과정에서 라쏘 모델의 성능지표가 릿지 모델에 비해 다소 낮게 나타났으며, 이를 해소하고자 라쏘 모델에 하이퍼파라메터인 알파값을 조절하여 라쏘 모델의 성능을 개선하였고, 그 결과 라쏘 모델의 성능이 릿지 모델보다 향상되었음을 확인할 수 있었다.
따라서, 특성공학을 포함한 정규화, 하이퍼파라메터 튜닝(알파값 조정)이 회귀 모델의 성능 향상에 기여할 수 있음을 확인하였다. 이러한 방법들을 통해 더욱 정교한 모델 구축이 가능할 것으로 기대된다.
'[파이썬] > 머신러닝' 카테고리의 다른 글
| [머신러닝] 훈련·검증·테스트 데이터로 분리하는 이유(+분리 비율) (1) | 2023.12.27 |
|---|---|
| [머신러닝] 데이터 특성 간 상관관계 확인 및 유의성 검정하기 (1) | 2023.12.26 |
| [머신러닝] 특성공학을 활용한 다중회귀모델 성능 향상(+예제, 해석, 개념) (0) | 2023.12.24 |
| [머신러닝] 선형회귀와 다항회귀 모델링의 이론과 실제 적용 방법(+예제) (1) | 2023.12.23 |
| [머신러닝] K최근접이웃모델(KNN) - 회귀분석의 기초(+ 예제) (0) | 2023.12.22 |




